Draw a Box-and-whisker Plot for the Following
Quartiles, Boxes, and Whiskers
For many computations in statistics, it is assumed that your data points (that is, the numbers in your listing) are clustered around some fundamental value; in other words, it is causeless that there is an "average" of some sort. The "box" in the box-and-whisker plot contains, and thereby highlights, the center portion of these data points.
To create a box-and-whisker plot, we beginning past ordering our information (that is, putting the values) in numerical social club, if they aren't ordered already. Then we find the median of our data.
The median divides the data into ii halves. To split the data into quarters, we then find the medians of these 2 halves.
Content Continues Below
Note: If we have an even number of values, so the offset median was the average of the 2 centre values, then we include the middle values in our sub-median computations. If we accept an odd number of values, so the first median was an actual data point, then we do not include that value in our sub-median computations. That is, to find the sub-medians, nosotros're only looking at the values that have not nevertheless been used.
And then nosotros have three points: the first center betoken (the median), and the middle points of the two halves (what I've been calling the "sub-medians"). These three points divide the entire data prepare into quarters, called "quartiles".
The top point of each quartile has a name, being a "Q" followed by the number of the quarter. So the top point of the starting time quarter of the data points is "Q1 ", and and so forth. Annotation that Q1 is as well the middle number for the commencement one-half of the list, Q2 is also the eye number for the whole list, Q3 is the middle number for the second half of the list, and Q4 is the largest value in the list.
Once nosotros have found these 3 points, Q1 , Q2 , and Q3 , we accept all we need in order to draw a simple box-and-whisker plot. Hither's an case of how it works.
-
Draw a box-and-whisker plot for the following information fix:
iv.3, 5.ane, 3.nine, 4.5, 4.4, iv.9, 5.0, iv.7, 4.1, four.6, 4.iv, four.iii, 4.8, 4.4, 4.2, iv.v, 4.4
My commencement step is to order the prepare. This gives me:
3.nine, iv.1, 4.two, iv.iii, four.3, 4.4, 4.4, 4.four, 4.4, 4.5, iv.five, 4.6, 4.vii, 4.eight, four.ix, v.0, five.1
The first value I need to find from this ordered listing is the median of the entire set. Since there are seventeen values in this list, the 9th value is the center value of the list, and is therefore my median:
3.nine, 4.one, four.2, 4.three, 4.iii, 4.4, iv.iv, 4.4,4.4,4.5, four.v, 4.6, 4.seven, 4.8, iv.ix, 5.0, five.1
3.9, iv.one, 4.2, four.three, 4.3, 4.four, 4.4, iv.iv, iv.4,4.5, 4.v, four.vi, 4.7, iv.8, 4.9, 5.0, five.ane
The median is Qtwo = iv.4
The adjacent two numbers I need are the medians of the ii halves. Since I used the "4.4" in the heart of the listing, I can't re-use information technology, so my two remaining data sets are:
3.9, four.i, 4.2, 4.three, four.3, four.4, 4.4, 4.iv
...and:
4.5, four.v, iv.six, four.vii, 4.viii, 4.9, 5.0, 5.one
The first one-half has 8 values, so the median is the average of the middle two values:
Q1 = (4.3 + four.3)/ii = 4.3
The median of the second half is:
Q3 = (iv.7 + four.viii)/2 = 4.75
To draw my box-and-whisker plot, I'll need to decide on a scale for my measurements. Since the values in my list are written with one decimal place and range from 3.9 to 5.one, I won't use a scale of, say, nada to 10, marked off past ones. Instead, I'll draw a number line from 3.fiveto5.5, and mark off by tenths.
![]()
(You might cull to measure from, say, iii to 6. Your choice would be equally adept as mine. The idea here is to be "reasonable", which allows you some flexibility.)
At present I'll marker off the minimum and maximum values, and Qi , Q2 , and Q3 :
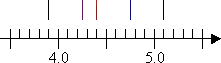
The "box" function of the plot goes from Q1 to Q3 , with a line fatigued inside the box to point the location of the median, Q2 :
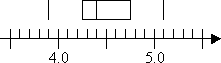
And so the "whiskers" are fatigued to the endpoints:
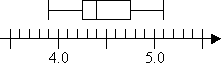
By the way, box-and-whisker plots don't have to be drawn horizontally equally I did above; they can be vertical, as well.
As mentioned at the commencement of this lesson, the "box" contains the middle portion of your data. As you can see in the graph above, the "whiskers" show how large is the "spread" of the data.
If you've got a wide box and long whiskers, and then maybe the information doesn't cluster as you'd hoped (or at least assumed). If your box is small-scale and the whiskers are short, then probably your data does indeed cluster. If your box is pocket-size and the whiskers are long, then perchance the data clusters, but you've got some "outliers" that you lot might need to investigate further — or, as nosotros'll come across later on, you may desire to discard some of your results.
-
Depict the box-and-whisker plot for the following data:
98, 77, 85, 88, 82, 83, 87
My beginning step is to order the information:
77, 82, 83, 85, 87, 88, 98
Next, I'll find the median. This set has seven values, and so the fourth value is the median:
Q2 = 85
The median splits the remaining data into two sets. The first set is 77, 82, 83. The median of this ready is:
Q1 = 82
The other set is 87, 88, 98. The median of this fix is:
Q3 = 88
I now take all the values I need for my box-and-whisker plot. At present I demand to effigy out what sort of calibration I'll use for this. Since all the values are 2-digit whole numbers, I won't bother with decimal places. Because the farthermost values (that is, the smallest and largest values) are 77 and 98 (20-ii units apart), I'll use 75 to 100 for min and max values, and I'll count by two'south for my scale. (There's null special about these values; they're just what feel "reasonable" to me. Your choices may differ. Just don't become using something silly like l to 150 or 76.5 to 98.ane.)
My set-up looks similar this:

The crooked portion at the bottom of the vertical centrality indicates that there is a portion of the number-line that'southward been omitted. In other words, this notation makes clear that the units for the vertical centrality do not start from zero.
(This zig-zag portion of the centrality appears generally to go past the name "zig-zag" or "break". If at that place's a proper term for this notation, I oasis't constitute it yet. The closest matter to a "standard" term for this sort of plot appears to exist "a broken-axis graph". I call the squiggly role of the axis "the hicky-bob thing".)
My next step is to draw the lines for the median (which is Q2 ) and the two sub-medians (existence the other quartiles, Qi and Qiii ), every bit well equally the two extremes:

And then I draw vertical lines to form my box and my whiskers:

I used a graphics program (and its "snap to grid" setting) to make my graphs above nice and bully. For your homework, use a ruler. And information technology would probably exist a adept idea to have a vi-inch (or fifteen-centimeter) ruler on mitt for your adjacent test. Yes, neatness counts.
Source: https://www.purplemath.com/modules/boxwhisk.htm